

| Es gibt eine Fülle von Möglichkeiten, Papier in zusammenhängende Polyeder zu falten und zu kleben. Dies können einfache oder verzweigte Ketten sein, ebene Gebilde aus vier- oder mehreckigen Polyedern, oder Raumgebilde. Sie lassen sich aber meist nicht umkrempeln. | |
| Die Ur-Form des Kaleidozyklus wurde 1958 vom Grafik-Design-Studenten Wallace G. Walker entdeckt, der an einem Projekt zur strukturellen Gestaltung von Papier arbeitete. |  US-Patent Nr. 3302321 (1967) |
| Das Ganze ähnelt einer Ziehharmonika, die ringförmig zusammengeklebt ist und umgekrempelt werden kann (mit etwas Mühe). |
 US-Patent Nr. 3302321 |
 US-Patent Nr. 3302321 |
 US-Patent Nr. 3302321 |
 |
| Bastelbogen: Die 12er Urform |
 |
Im Lauf der Zeit wurde daraus eine Vielzahl von besser funktionierenden Varianten dieses schönen Objekts entwickelt. | Im Wesentlichen handelt es sich um geschlossene Ketten von Tetraedern (Einzahl: Tetraeder, sprich: "Tetra-Eder"; nicht "Teträder", oder gar "Treträder"). |
| Bei einem Tetraeder bestehen die 4 Flächen aus gleichseitigen Dreiecken. Es ist der Einfachste der 5 platonischen Körper und wird auch "dreiseitige regelmäßige Pyramide" oder "gleichseitiger Simplex" genannt. Verbindet man gleich große Tetraeder an ihren jeweils gegenüberliegenden Kanten mit einem Scharnier (z. B. Klebeband), entsteht eine bewegliche Kette. | 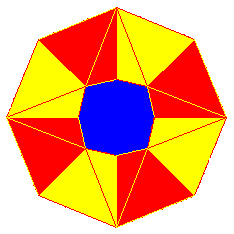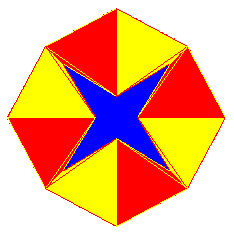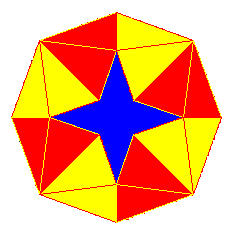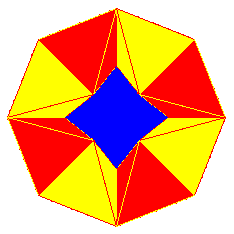 |
Manche dieser Tetraeder-Ketten lassen sich ringförmig zu einem Kaleidozyklus zusammenfügen und krempeln. Sie müssen dann aus einer ganzzahligen Anzahl Tetraedern bestehen, mindestens jedoch aus 8 Stücken. Diese Sorte Kaleidozyklen besitzt ein stets offenes (hier: blaues) "Auge" und ist insgesamt ziemlich wacklig. |
 |
||
| Bastelbogen: Der 8er offen |
| Besteht ein Tetraeder aus 4 gleichschenkligen Dreiecken, wird er meist nicht mehr Tetraeder genannt, sondern "dreiseitige schiefe Pyramide" oder "gleichschenkliger Simplex". | Mit solcherart gestreckten Tetraedern (Simplices) können Kaleidozyklen erzeugt werden, deren "Auge" bei bestimmten Positionen geschlossen ist. Sie sind insgesamt weniger wacklig. |  |
||
| Bastelbogen: Der 8er geschlossen |
|
... und :
Es lassen sich umkrempelbare Ringe aus nur 6 Simplices herstellen! Dies ist die Mindestzahl, weniger geht nicht; sie sind nicht wacklig. Kein Bastelbogen für den offenen 6er da er nicht so spannend ist. |
 GB-Patent Nr. 588842 (1947) |
| Sehr viel besser ist der 6er-Kaleidozyklus mit geschlossenem Auge, der Standard-Krempler! | ||
 US-Patent Nr. 1997022 (1935) US-Patent Nr. 3611617 (1968) |
 US-Patent Nr. 2688820 (1954) |
 |
| Bastelbogen: Der 6er geschlossen und noch einer |
||
| http://www.mathematische-basteleien.de/kaleidozyklen.htm http://www.kentuckycrafts.org/susan_wood.htm |
| Mit Ketten aus rechtwinkligen Simplices (deren Flächen nur aus rechtwinkligen Dreiecken bestehen) lassen sich "Umstülpgürtel" erzeugen. Der einfachste dieser Gürtel ist der "umstülpbare Würfelgürtel nach Paul Schatz". | 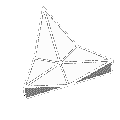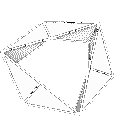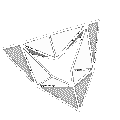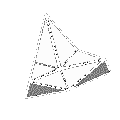 |
Die seltsam-schöne Bewegung des Würfelgürtels beflügelt die Phantasie und hat Einfluss auf die polysomatische Architekturgestaltung, die Rhythmusforschung, eine neue, naturfreundliche Maschinenbaukunst, die eurythmische Kunst... |
| http://www.fzk.at/index.html http://www.a.tu-berlin.de/student/florian/an.htm http://www.thurgautravel.ch/inv/de/index.htm |
| Zur Konstruktion eines Simplex für einen Krempel-Hexaeder-Gürtel nehme man ein gleichseitiges Dreieck und teile es in 6 rechtwinklige Dreiecke. |  |
| Um einen Simplex falten zu können, hefte man 3 weitere, "passende" Dreiecke daran, schneide das Ganze aus, falte es an den Linien und klebe es zusammen. |  |
| Das Ganze mache man 6 mal und klebe die Simplices zu einem Ring zusammen. | |
| Aus einem gleichseitigen Viereck entsteht auf die gleiche Weise ein Krempel-Oktaeder-Gürtel. Umstülpbarer Oktadergürtel nach Wundersames. |
 |
 |
Bastelbogen: Hexaeder-Gürtel |
Bastelbogen: Oktaeder-Gürtel |
| Aus einem gleichseitigen Fünfeck entsteht ein ... ? |
 |
| Je mehr Kettenglieder in einem Kaleidozyklus vorhanden sind, um so mehr verwandelt er sich in ein Puzzle. Durch Zusammenlegen der Simplices entsteht eine Fülle von geometrischen Formen. | Die 6-gliedrigen sind keine Puzzles, die 8-gliedrigen sind deutlich vielfältiger, die 10er noch sehr viel mehr etc. Ein Kaleidozyklus ist nur noch mit Mühe zu erkennen. |
| Aus der Vielzahl der vielteiligen Kaleidozyklen erwähne ich hier nur zwei, beide gut vermarktet. | ||
| Triamant |  |
 |
| WO-Patent Nr. 1992011911 (1992) | ||
| Kubus X | In der Patentschrift wird eine komplette "Polyeder-Puzzle-Familie" beschrieben (Tetraeder, Hexaeder, Oktaeder, Dodekaeder...) . |
 EP-Patent Nr. 787514 (1997) |
| Und dann noch: http://www.mathematische-basteleien.de/shinsei.htm | ||
| Eine weitere Verallgemeinerung besteht in der Verwendung von orthogonalen Simplices, bei denen es darauf ankommt, dass deren "Scharnier-" Kanten senkrecht zueinander stehen. |
 |
http://www.kulturata.de/de/dept_20.html Link leider defekt. |
 |
Letzte Änderung 13.3.2005 |